
שם הסטודנט
:
יצחק ביבי
: מנחה
וולדימיר אוסטרובסקי
הנדסת חשמל
פיתוח סביבת תכנון של מערכת צירופית עם תיקון
שגיאות בזמן אמת
מהות
: המחקר
בפרויקט
נעסוק אנו זה מחקרי
בשיטה
חדשה
מסוג
ECOC
אשר
מהווה
בדיקה
ותיקון
שגיאות
רנדומאליות
וכן
לתיקון
שגיאות
לליקויים
בתוך
המעגל
הפונקציונאלי
,
כלומר
בסכמת
, המערכת
ללא
התערבות
פנימית
בתהליכי
המערכת
הנבדקת
נבדוק אנו .
יעילות את
האלגוריתם
הן ,
מבחינת
משאבי
חומרה
והן
מבחינת
ביצועים
וזמן
. הרצה
שאלת המחקר
:
האם ניתן לבנות מערכת לתיקון שגיאות מסוג
ECOC
עבור אות כניסה עם אי תלות פונקציונאלית אשר
באפשרותה לשפר את האלגוריתם הקיים בשוק ובנוסף האם ניתן למצוא
,
עבור כל גורמי החופש
האפשרים באלגוריתם הנבדק
,
את המודל האופטימאלי עם מינימום אלמנטים לוגיים לתיקון וזמן
השהייה מינימלי
?
מטרות המחקר
:
מציאת יחסי הגומלין בין משאבי חומרה לבין הביצועים וזמן הרצה
.
בחירה של מודל תיקון שגיאות אופטימאלי הבודק
:
*
מינימום סיביות למשתני בדיקה
.
*
מינימום שדות במטריצה הנבחרת
מציאה ותיקון שגיאה רנדומאלית ושגיאה סכמתית
.
יעדי המחקר
:
תכנון מערכת סיפרתית צירופית עם חומרה לתיקון שגיאות אשר מבצעת
:
1.
אלגוריתם יצירת מודלים תוכנתיים אשר ניתן לשינוי היחס בין השדות למשתני הבדיקה אשר יתבצע
"ע
י קוד שפת
C++
2.
בחירת מודל תיקון שגיאות אופטימאלי עם מינימום משתני בדיקה אשר יומר לקוד שפת
VHDL
3
.
המודול הנבחר יבנה ע
י "
Quartus
ויתחשב במספר קריטריונים
:
*
מינימום אלמנטים לוגיים
.
*
מינימום זמן השהייה לתיקון
.
אשר מבצע יחס גומלין בין משאבי החומרה לביצועים והעונה לרוב הדרישות המעשיות
.
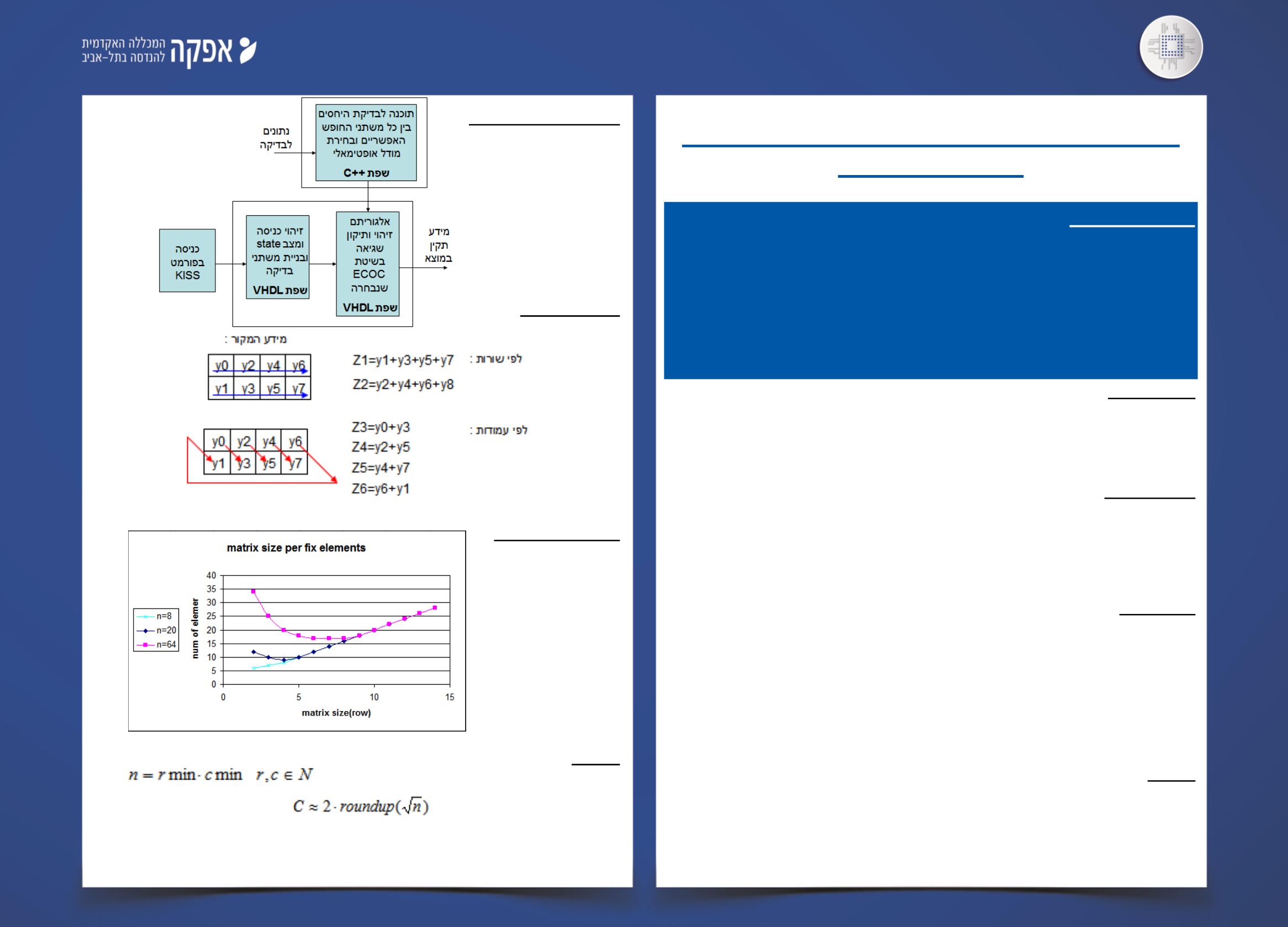
: השיטה
לשיטה אין מסגרת קבועה לתיקון שגיאה וניתן לשנות אותה בהתאם לצורכנו תוך שמירה על חוקיות
החלוקה לשדות של המערכת
.
בפרויקט אנו מחלקים את סיביות המידע של המערכת הנבדקת
למטריצה
,
המערכת עושה בדיקה בין המידע שצפוי לצאת לבין המטריצה הנבדקת
.
המערכת מבצעת את פעולת התיקון תוך כדי מציאת האיזון הטוב ביותר בין מינימום מספר השדות
במודולים השונים ומינימום מספר משתני הבדיקה לעומת עלויות החומרה לשם ביצועים מיטביים
.
כלומר המחקר צריך לבחור מודל תיקון שגיאות אופטימאלי אשר עונה לרוב הדרישות המעשיות
.
סכמת מלבנים של המערכת
אלגוריתם הפענוח
בדיקות ותוצאות מחקר
: מסקנות
*
גודל המטריצה המינימאלית נמצאה לפי נקודת הברך
:
*
כמות אלמנטים לבדיקה נע לפי
:
*
גודל הבלוק
,
by
,
הינו ככמות השורות
,
r
,
לכן כמות התקלות שניתן למצוא הוא מקסימום
r
*
זמן ההשהייה המקסימאלי
tpd
הינו עד
4dt
,
כאשר
dt
הינו זמן השהייה של רכיב לוגי אחד
.
*
האלגוריתם חוסך עד
60%
רכיבים מהשיטה
majority
המקובלת בשוק
.
















